INTRODUCTION: Samos, Polycratis, Efpalinos, 6th century B.C.
Approximately 2,500 years ago, during the 2nd half of the 6th century B.C., the island of Samos was governed by the notorious Tyrant Polycratis. Samos was a distinguished naval power and thus experienced great economic and political prosperity.
Polycratis commissioned unique technical works, which were partly aimed at meeting the needs of the inhabitants of the island and his army, and partly at projecting his superiority to allies as well as enemies. Some of the works that have been attributed to Polycratis are: The GreatTemple of Hera, the largest of its time, with 115 columns, the sea wall of the port, with a length of 360 meters and built on foundations at a depth of 40 meters, the circumvallation of the city and the aqueduct of the ancient city of Samos.
Polycratis commissioned the study and the design of the aqueduct to one of the most distinguished architects of his time,Efpalinos of Megara. Efpalinos designed and constructed a system for the convection of water, via natural flow, from a source located quite far away from the city.
The system consists of a horizontal tunnel with a length of 1,035 meters, which goes through a mountain. What is remarkable about this is that the excavation of the tunnel which began simultaneously on both sides of the hill was completed with precision. The study and construction of the work was based on his previous experience in the construction of aqueducts (Athens, Korinth, Megara), on the ancient science of mathematics, which at the time had made its great leap, and on the use of sighting devices.
The work, which was pioneering for the world at the time and remained unmatched for centuries, constituted a top most technical achievement comparable to which are only modern works. The perfection of its construction and the soundness of its technical specs are proven by the fact that the aqueduct functioned for 1,000 years and with proper maintenance, could have functioned up to this day. Today the aqueduct constitutes an exceptional monument to ancient applied geometry in the core of the most beautiful, according to Herodotus, Greek city, Samos.
THE WORK: `The Tunnel of Efpalinos`
The terminus of the work was the construction of a subterranean duct which would carry water from a source, known today as the Agiathes source, to the city of ancient Samos, penetrating the mountain which stood between them.
Efpalinos,* who was summoned by Polycratis,** came to Samos and after discussing the specifications of the project and finding that the source was located on a higher level than the city, decided on the manner of its construction.
* Efpalinos must have been a renowned hydraulics engineer (water supply, drainage, etc.) and must have been called by Polycratis as an authority in these types of projects. It is probable that he also participated in the construction of the aqueduct of Theagenis in Megara (540 B.C.) thus becoming famous throughout Greece.
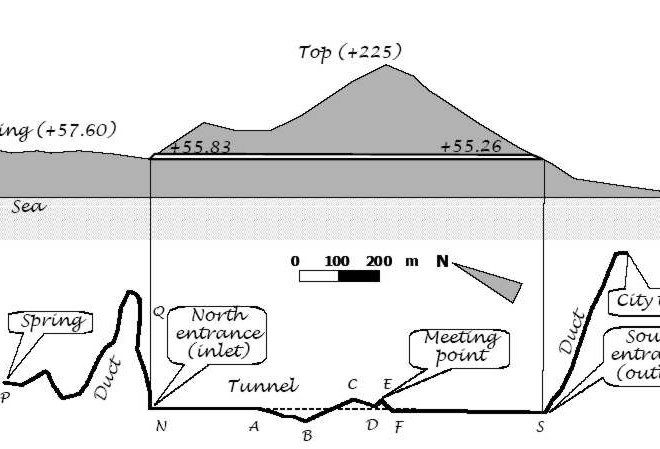
The project was to be subterranean (for security purposes in the event of a siege). The duct was to have an average inclination of 0.6%. The route of the duct (fig.1) would be:
-859 meters from the source to the mountain, through a subterranean structured ditch,
-1,035 meters through a tunnel that would be cut into the mountain and
-520 meters from the mountain to the reservoir of the city, through another ditch.
The water from the source would be collected in a reservoir half of which would be chiseled into the rock and the rest built. From there, a series of ducts placed in a subterranean structured ditch would carry the water towards the tunnel of the mountain and from there to the reservoir of the city.
The most difficult part of the project, which demanded serious study and precision, was the opening of the 1,035 meter tunnel which would penetrate the mountain. It was decided that this would be constructed:
-horizontally (for fear of subterranean waters),
-rectilinear (at a height of +55.8 meters above sea level) and
-“double-entranced” (by digging simultaneously on both sides to save time)
On the floor of the horizontal tunnel a sloped ditch would be constructed, through which the water would be carried to the reservoir of the city via clay pipes (fig.2).
The project was completed in approximately ten years (probably from 530 B.C. to 520 B.C.) and began to function, carrying water from the source to the city through clay pipes (26 centimeters in diameter) from a distance of 2,400 meters.
This aqueduct functioned until the 5th century A.D., but was then abandoned probably due to maintenance problems. Then the Roman aqueduct was constructed on the surface of the mountain and around its perimeter, which continued to supply the city with water until the previous century.
The ancient source continues to supply the city of Pythagorion with 250 cubic meters of water every 24 hours.
The fact that this work was forgotten and remained unknown for fourteen centuries is due, among other things, to the fact that it was completely subterranean and that no written testimony of its existence was ever found except for a brief reference by Herodotus (440 B.C.).
** Polycratis lived during the 6th century B.C. He assumed power in 538 B.C. together with his brothers Pantagnostos and Sylosontas, whom he ousted, though, in 532 B.C. Relying on a mercenary army and on the new type of ship he built, the famous Samaina, he succeeded in placing many neighboring islands and parts of the coast of Asia Minor under his influence. He had developed friendly relations with many powerful sovereigns of the time, such as the Pharaoh of Egypt Amasis. Polycratis` policy forced some of the aristocrats of Samos, such as the philosopher Pythagoras to abandon the island. In 533 B.C. Polycratis was captured by the Persian autocrat Oroitis in Magnesia of the Meander, where he was arrested, put to death and his corpse hung on a cross. The means of his demise left a great impression on the then known world.
HERODOTOS: Reference to The Tunnel of Efpalinos
Herodotus (approximately 480-426 B.C.) in his “Stories” (C, 60) writes:
“the excavation of the tunnel started simultaneously from both sides of the mountain”, “I spoke though, more about the people of Samos because they constructed three works, which were the largest of those constructed in the whole of Greece; under a mountain, as high as 150 fathoms ( =227m), a tunnel with two entrances was constructed. The length of the tunnel is seven stadiums ( = 7×185=1,295m), it’s height and width is 8 feet (8 feet = 2.48m), through which the water from a great source is carried by pipes to the city. The engineer of this tunnel was Efpalinos from Megara, son of Nafstrofos…”
This was the only piece of information on this great construction available to archaeologists in the previous century. In this text the location of the tunnel is not mentioned, but it is implied that the mountain was the one north of the city, moreover the location of the source is not mentioned either. During those times the location of the ancient spring was lost since two small chapels had been built over it, while its water, due to sedimentation of the aqueduct, welled up many meters further down becoming lost through the pebbles of St. John’s Stream.
Herodotus, who had visited the aqueduct and the tunnel, knew that it was horizontal and “double-entranced”, that is, its excavation was carried out from both sides of the mountain. Surely however, he was not aware of the fact that the tunnel was rectilinear. This is the most remarkable of its characteristics, which, if he had known, would surely have mentioned.
Without Herodotus` reference however, it is likely that this monument of ancient Greek topography would never have been discovered. Following the translation of Herodotus in Europe, the search for the tunnel by archeologists and excursionists began, until finally the French archeologist Honoree Victor Guerin, with the help of Chieftain Alexis, discovered the spring and the beginning of the aqueduct in 1856. In 1882, with the expenses being covered by the people of Samos and under the guidance of the monks Theophanous Areli and Kyrillos, this wonderful work was fully disclosed in its entirety. The first mapping was done in 1884 and for the first time since ancient days, the fact that the two tunnels were rectilinear was confirmed. The restoration of the tunnel was completed and a detailed plan of it was made during the 1970`s. Today it is lighted but only the south side of the tunnel can be visited.
Since no original scientific texts of the 6th century B.C. have been preserved, The Tunnel of Efpalinos constitutes valuable living testimony and offers evidence with which we are able to reconstruct a coherent image of scientific life during that century.
The mathematical interest of this work lies in the measurements that were made by Efpalinos, as well as the geometrical problems that he solved, in order to implement his plans onto the landscape and to complete the project. Two of the primary problems were:
A. He had to construct the route of the duct based on the inclination he had chosen (0.6%), according to the existing ground relief.
B. He had to determine the two ends of the tunnel on both slopes of the mountain, so that they would be on the same altitude, and the direction of excavation which would be followed by the two teams in order to bore through the mountain.
The relatively steady slope of the duct through its entire length, as well as the maintaining of the two tunnels both horizontal and absolutely rectilinear, prove the existence of some kind of ancient sighting device that was used for the supervision of the work. Given the fact that the main geometrical instrument of the time was the plumb line, Efpalinos` sighting device must have had the form of figure 6.
6th Century B.C. The age of Thalis and Pythagoras
Dominant figures in the intellectual field of the 6th century B.C. were Thalis of Militos and Pythagoras of Samos.
Thalis was born in Militos of Ionia around 640 B.C. and died also in Militos around 546 B.C. He is considered to be the first philosopher and father of mathematics in the contemporary sense of the term. The concepts of “angles” and “parallels” as well as the introduction of “proof” in mathematics, which may well be the greatest conceptions of the human mind, are attributed to Thales. He was a scholar in every sense of the ancient word; he was not only a theorist and philosopher, but also a man with practical thought. Thalis and other Ionian mathematicians of the time cultivated the science of mathematics not only for its interest, but also due to its practical applications.
The proofs to the following geometrical theorems are attributed to Thales:
– The diameter divides the circle in two equal parts
– The vertexes of a triangle are equal
– The base angles of an isosceles triangle are equal
– The angle defined by the semi-circumference of a circle is right (90o)
– If two triangles have one equal side and their adjacent angles are equal, then they are equal
– Other theorems relevant to similar triangles
Thales dealt with some of his theorems in a more general way while with others in a way more comprehensible by the senses and still others he demonstrated to his apprentices.
Pythagoras was born in Samos around 580 B.C. He went into exile due to contrariety to the Tyranny of Polykratis and went to Sicily in 535 B.C. There he lived in various cities in the area and finally around 525 B.C. settled in Croton, where he established a philosophical school and religious cult known as Pythagorism. He was ousted from Croton along with his students however, and settled in Metapontion where he died soon afterwards, around 500 B.C. His followers, known as Pythagorists, continued his work and enriched the theories of their teacher legating to the next generations of scholars some very fertile concepts.
The life of Pythagoras and the origins of Pythagorism are surrounded by a thick vale of legends and partly historical traditions. Pythagoras set mathematics apart from the practical applications as they were associated by the Ionian Mathematicians until then, by giving them a form of free study. He reviewed the principles of geometry from a higher point of view and investigated its theorems in an incorporeal and spiritual way. The Pythagoreans, through mathematics, sought a sort of religious envisagement – a way of reaching the infinite truth.
They were interested in some theories as far as geometrical forms were concerned, such as the Pythagorean Theorem, and concepts such as the point, the line, the triangle and the tetrahedron.
The following are attributed to the Pythagoreans:
– The Theory of the surds
– The constitution of cosmic schemes (i.e. the regular polyhedrons )
– The mathematical proof of the Pythagorean theorem
– The theorem: “The sum of the angles of a triangle is equal to two right angles”
SAMOS
In the outermost eastern part of the Aegean and 18 miles from the coast of Asia Minor lies the island of Samos. It covers an area of 476 square kilometers, with a coastal line of 159 kilometers and is 175 nautical miles from Piraeus. It has a population of 40.519 inhabitants. Geologically the island was formed following great tectonic activity in the area, a result of which was its separation from the Asia Minor mainland with which it was united (quaternary era).
Around 1100 B.C., Ionian settlers arrived on the island. The hay day of the island was during the 5th and 6th centuries BC, especially from 540 BC when the Tyrant Polycrates became the ruler of the island. During the Persian wars it was conquered by the Persians and later it became part of the first Athenian alliance. In 440 BC Samos defected from the alliance which resulted in the Athenians attacking and desolating the island. During the Peloponnesian Wars Samos fought on the side of Athens against Sparta and following that, came successively under Macedonian, the Ptolemy of Egypt and Roman rule. During the Byzantine era it was part of the district of the Aegean and faced a period of decline since it was pestered by pirate raids. After Constantinople was seized by the Franks in 1204, it came successively under the rule of the Franks, the Venetians and from 1413, the Genuates when the Justiniani became the owners of the island.
After the fall of Constantinople to the Turks in 1453 the inhabitants abandon the island and seek refuge in Chios Island. Samos remains deserted until the middle of the 16th century whereupon the Turkish Pasha who took the island under his patronage, managed, by giving various motives, (i.e. privileges, self government, religious freedom) to attract new inhabitants and thus succeeded in its re-colonization. Although Samos played an active role during the Greek Revolution in 1821, it only became part of Greece in 1912, holding a status of a special autonomic Hegemony under Turkey until then. During the Second World War however, the island once again suffered great destruction.
This is a link of Efpalinos tunnel
 iSamos.gr Η ενημερωτική σελίδα της Σάμου! Εξερευνήστε τη Σάμο, τις παραλίες της, τη φύση της, τις ομορφιές της. Διαβάστε την ιστορία της Σάμου
iSamos.gr Η ενημερωτική σελίδα της Σάμου! Εξερευνήστε τη Σάμο, τις παραλίες της, τη φύση της, τις ομορφιές της. Διαβάστε την ιστορία της Σάμου